ĪĪĪĪĮŌŻ║╚²ĮŪą╬ABD┼c╚²ĮŪą╬ADCĄ─Ė▀ŽÓ═¼.
ĪĪĪĪ╚²ĮŪą╬ABD├µĘe=4Ī┴Ė▀Ī┬2.
ĪĪĪĪ╚²ĮŪą╬ ADC├µĘe=2Ī┴Ė▀Ī┬2.
ĪĪĪĪę“┤╦╚²ĮŪą╬ABDĄ─├µĘe╩Ū╚²ĮŪą╬ADC├µĘeĄ─2▒Č.ūóęŌŻ║╚²ĮŪą╬Ą─╚╬ęŌę╗▀ģČ╝┐╔ęį┐┤ū„╩ŪĄū��Ż¼▀@Śl▀ģ╔ŽĄ─Ė▀Š═╩Ū╚²ĮŪą╬Ą─Ė▀��Ż¼╦∙ęį├┐éĆ╚²ĮŪą╬Č╝┐╔┐┤│╔ėą╚²éĆĄūŻ¼║═ŽÓæ¬(y©®ng)Ą─╚²ŚlĖ▀.
ĪĪĪĪ└²2 ėęłDųą��Ż¼BD��Ż¼DE�����Ż¼ECĄ─ķLĘųäe╩Ū2��Ż¼4���Ż¼2.F╩ŪŠĆČ╬AEĄ─ųą³cŻ¼╚²ĮŪą╬ABCĄ─Ė▀×ķ4.Ū¾╚²ĮŪą╬DFEĄ─├µĘe.
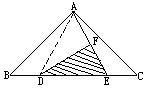
ĪĪĪĪĮŌŻ║ BCŻĮ 2Ż½ 4Ż½ 2ŻĮ 8.
ĪĪĪĪ╚²ĮŪą╬ ABC├µĘe= 8Ī┴ 4Ī┬2ŻĮ16.
ĪĪĪĪ╬ęéā░čA║═D▀B│╔ŠĆČ╬��Ż¼ĮM│╔╚²ĮŪą╬ADE���Ż¼╦³┼c╚²ĮŪą╬ABCĄ─Ė▀ŽÓ═¼�Ż¼Č°DEķL╩Ū4�����Ż¼ę▓╩ŪBCĄ─ę╗░ļ�Ż¼ę“┤╦╚²ĮŪą╬ADE├µĘe╩Ū╚²ĮŪą╬ABC├µĘeĄ─ę╗░ļ.═¼śėĄ└└ĒŻ¼EF╩ŪAEĄ─ę╗░ļŻ¼╚²ĮŪą╬DFE├µĘe╩Ū╚²ĮŪą╬ADE├µĘeĄ─ę╗░ļ.
ĪĪĪĪ
ĪĪĪĪ╚²ĮŪą╬ DFE├µĘe= 16Ī┬4ŻĮ4.
ĪĪĪĪ└²3 ėęłDųąķLĘĮą╬Ą─ķL╩Ū20����Ż¼īÆ╩Ū12Ż¼Ū¾╦³Ą─ā╚(n©©i)▓┐ĻÄė░▓┐Ęų├µĘe.

ĪĪĪĪĮŌŻ║ABEFę▓╩Ūę╗éĆķLĘĮą╬�����Ż¼╦³ā╚(n©©i)▓┐Ą─╚²éĆ╚²ĮŪą╬ĻÄė░▓┐ĘųĖ▀Č╝┼cBEę╗śėķL.
ĪĪĪĪČ°╚²éĆ╚²ĮŪą╬Ąū▀ģĄ─ķL╝ėŲüĒ����Ż¼Š═╩ŪFEĄ─ķL.ę“┤╦▀@╚²éĆ╚²ĮŪą╬Ą─├µĘeų«║═╩Ū
ĪĪĪĪFEĪ┴BEĪ┬2Ż¼
ĪĪĪĪ╦³ŪĪ║├╩ŪķLĘĮą╬ABEF├µĘeĄ─ę╗░ļ.
ĪĪĪĪ═¼śėĄ└└Ē����Ż¼F(xi©żn)ECDę▓╩ŪķLĘĮą╬Ż¼╦³ā╚(n©©i)▓┐╚²éĆ╚²ĮŪą╬Ż©ĻÄė░▓┐ĘųŻ®├µĘeų«║═╩Ū╦³Ą─├µĘeĄ─ę╗░ļ.
ĪĪĪĪę“┤╦╦∙ėąĻÄė░Ą─├µĘe╩ŪķLĘĮą╬ABCD├µĘeĄ─ę╗░ļ�����Ż¼ę▓Š═╩Ū
ĪĪĪĪ20Ī┴12Ī┬2ŻĮ120.
ĪĪĪĪ═©▀^ĘĮĖ±╝ł�Ż¼╬ęéā▀Ć┐╔ęįÅ─┴Ēę╗éĆ═ŠÅĮüĒŪ¾ĮŌ.«ö(d©Īng)╬ęéā«ŗ│÷ųąķgā╔éĆ╚²ĮŪą╬Ą─Ė▀ŠĆŻ¼░č├┐éĆ╚²ĮŪą╬Ęų│╔ā╔éĆų▒ĮŪ╚²ĮŪą╬║¾���Ż¼łDųą├┐éĆų▒ĮŪ╚²ĮŪą╬Č╝╩Ū─│éĆķLĘĮą╬Ą─ę╗░ļ�����Ż¼Č°ķLĘĮą╬ABCD╩Ūė╔▀@╚¶Ė╔éĆķLĘĮą╬Ų┤│╔.ę“┤╦╦∙ėą▀@ą®ų▒ĮŪ╚²ĮŪą╬Ż©ĻÄė░▓┐ĘųŻ®Ą─├µĘeų«║═╩ŪķLĘĮą╬ABCD├µĘeĄ─Ą─ę╗░ļ.
ĪĪĪĪ└²4 ėęłDųą��Ż¼ėą╦─ŚlŠĆČ╬Ą─ķLČ╚ęčĮø(j©®ng)ų¬Ą└�Ż¼▀Ćėąā╔éĆĮŪ╩Ūų▒ĮŪ�����Ż¼─Ū├┤╦─▀ģą╬ABCDŻ©ĻÄė░▓┐ĘųŻ®Ą─├µĘe╩ŪČÓ╔┘�Ż┐

ĪĪĪĪĮŌŻ║░čA║═C▀B│╔ŠĆČ╬Ż¼╦─▀ģą╬ABCDŠ═Ęų│╔┴╦ā╔éĆ�����Ż¼╚²ĮŪą╬ABC║═╚²ĮŪą╬ADC.
ĪĪĪĪī”╚²ĮŪą╬ABCüĒšf���Ż¼AB╩ŪĄū▀ģ����Ż¼Ė▀╩Ū10�����Ż¼ę“┤╦
ĪĪĪĪ├µĘe=4Ī┴10Ī┬2ŻĮ 20.
ĪĪĪĪī”╚²ĮŪą╬ ADCüĒšfŻ¼ DC╩ŪĄū▀ģ����Ż¼Ė▀╩Ū 8Ż¼ę“┤╦
ĪĪĪĪ├µĘe=7Ī┴8Ī┬2ŻĮ28.
ĪĪĪĪ╦─▀ģą╬ ABCD├µĘe= 20Ż½ 28ŻĮ 48.
ĪĪĪĪ▀@ę╗└²Ņ}į┘ę╗┤╬ĖµįV╬ęéā���Ż¼ŌgĮŪ╚²ĮŪą╬Ą─Ė▀ŠĆėą┐╔─▄╩Ūį┌╚²ĮŪą╬Ą─═Ō├µ.
ĪĪĪĪ└²5 į┌▀ģķL×ķ6Ą─š²ĘĮą╬ā╚(n©©i)ėąę╗éĆ╚²ĮŪą╬BEF�����Ż¼ŠĆČ╬AEŻĮ3�����Ż¼DFŻĮ2�Ż¼Ū¾╚²ĮŪą╬BEFĄ─├µĘe.
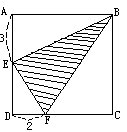
ĪĪĪĪĮŌŻ║ę¬ų▒ĮėŪ¾│÷╚²ĮŪą╬BEFĄ─├µĘe╩Ū└¦ļyĄ─��Ż¼Ą½╚▌ęūŪ¾│÷Ž┬├µ┴ąĄ─╚²éĆų▒ĮŪ╚²ĮŪą╬Ą─├µĘe
ĪĪĪĪ╚²ĮŪą╬ ABE├µĘe=3Ī┴6Ī┴2ŻĮ 9.
ĪĪĪĪ╚²ĮŪą╬ BCF├µĘe= 6Ī┴Ż©6-2Ż®Ī┬2ŻĮ 12.
ĪĪĪĪ╚²ĮŪą╬ DEF├µĘe=2Ī┴Ż©6-3Ż®Ī┬2ŻĮ 3.
ĪĪĪĪ╬ęéāų╗ę¬ė├š²ĘĮą╬├µĘe£p╚ź▀@╚²éĆų▒ĮŪ╚²ĮŪą╬Ą─├µĘeŠ═─▄╦Ń│÷Ż║
ĪĪĪĪ╚²ĮŪą╬ BEF├µĘe=6Ī┴6-9-12-3ŻĮ12.
ĪĪĪĪ└²6 į┌ėęłDųą��Ż¼ABCD╩ŪķLĘĮą╬����Ż¼╚²ŚlŠĆČ╬Ą─ķLČ╚╚ńłD╦∙╩ŠŻ¼M╩ŪŠĆČ╬DEĄ─ųą³c����Ż¼Ū¾╦─▀ģą╬ABMDŻ©ĻÄė░▓┐ĘųŻ®Ą─├µĘe.

ĪĪĪĪĮŌŻ║╦─▀ģą╬ABMDųą����Ż¼ęčų¬Ą─╠½╔┘���Ż¼ų▒ĮėŪ¾╦³├µĘe╩Ū▓╗┐╔─▄Ą─�����Ż¼╬ęéāįO(sh©©)Ę©Ū¾│÷╚²ĮŪą╬DCE┼c╚²ĮŪą╬MBEĄ─├µĘeŻ¼╚╗║¾ė├ķLĘĮą╬ABCDĄ─├µĘe£p╚ź╦³éā�Ż¼ė╔┤╦Š═┐╔ęįŪ¾Ą├╦─▀ģą╬ABMDĄ─├µĘe.
ĪĪĪĪ░čM┼cCė├ŠĆČ╬▀BŲüĒŻ¼īó╚²ĮŪą╬DCEĘų│╔ā╔éĆ╚²ĮŪą╬.╚²ĮŪą╬ DCEĄ─├µĘe╩Ū 7Ī┴2Ī┬2ŻĮ7.
ĪĪĪĪę“×ķM╩ŪŠĆČ╬DEĄ─ųą³c����Ż¼╚²ĮŪą╬DMC┼c╚²ĮŪą╬MCE├µĘeŽÓĄ╚Ż¼╦∙ęį╚²ĮŪą╬MCE├µĘe╩Ū 7Ī┬2ŻĮ3.5.
ĪĪĪĪę“×ķ BEŻĮ 8╩Ū CEŻĮ 2Ą─ 4▒Č��Ż¼╚²ĮŪą╬ MBE┼c╚²ĮŪą╬MCEĖ▀ę╗śė����Ż¼ę“┤╦╚²ĮŪą╬MBE├µĘe╩Ū
ĪĪĪĪ3.5Ī┴4ŻĮ14.
ĪĪĪĪķLĘĮą╬ ABCD├µĘe=7Ī┴Ż©8Ż½2Ż®=70.
ĪĪĪĪ╦─▀ģą╬ ABMD├µĘe=70-7- 14ŻĮ 49.
Č■ĪóėąĻP(gu©Īn)š²ĘĮą╬Ą─å¢Ņ}
ĪĪĪĪŽ╚Å─Ą╚č³ų▒ĮŪ╚²ĮŪą╬ųvŲ.
ĪĪĪĪę╗éĆų▒ĮŪ╚²ĮŪą╬�Ż¼╦³Ą─ā╔Ślų▒ĮŪ▀ģę╗śėķL�Ż¼▀@śėĄ─ų▒ĮŪ╚²ĮŪą╬�����Ż¼Š═Įąū÷Ą╚č³ų▒ĮŪ╚²ĮŪą╬.╦³ėąę╗éĆų▒ĮŪŻ©90Č╚Ż®����Ż¼▀Ćėąā╔éĆĮŪČ╝╩Ū45Č╚Ż¼═©│Żį┌ę╗Ė▒╚²ĮŪ│▀ųą.ėąę╗éĆŠ═╩ŪĄ╚č³ų▒ĮŪ╚²ĮŪą╬.
ĪĪĪĪā╔éĆę╗śėĄ─Ą╚č³ų▒ĮŪ╚²ĮŪą╬�Ż¼┐╔ęįŲ┤│╔ę╗éĆš²ĘĮą╬Ż¼╚ńłDŻ©aŻ®.╦─éĆę╗śėĄ─Ą╚č³ų▒ĮŪ╚²ĮŪą╬�Ż¼ę▓┐╔ęįŲ┤│╔ę╗éĆš²ĘĮą╬Ż¼╚ńłDŻ©bŻ®.
ĪĪĪĪę╗éĆĄ╚č³ų▒ĮŪ╚²ĮŪą╬��Ż¼«ö(d©Īng)ų¬Ą└╦³Ą─ų▒ĮŪ▀ģķL�����Ż¼Å─łDŻ©aŻ®ų¬����Ż¼╦³Ą─├µĘe╩Ū
ĪĪĪĪų▒ĮŪ▀ģķLĄ─ŲĮĘĮĪ┬2.
ĪĪĪĪ«ö(d©Īng)ų¬Ą└╦³Ą─ą▒▀ģķLŻ¼Å─łDŻ©bŻ®ų¬����Ż¼╦³Ą─├µĘe╩Ū

ĪĪĪĪą▒▀ģĄ─ŲĮĘĮĪ┬4
ĪĪĪĪ└²7 ėęłDė╔┴∙éĆĄ╚č³ų▒ĮŪ╚²ĮŪą╬ĮM│╔.Ą┌ę╗éĆ╚²ĮŪą╬ā╔Ślų▒ĮŪ▀ģķL╩Ū8.║¾ę╗éĆ╚²ĮŪą╬Ą─ų▒ĮŪ▀ģķL���Ż¼ŪĪ║├╩ŪŪ░ę╗éĆą▒▀ģķLĄ─ę╗░ļŻ¼Ū¾▀@éĆłDą╬Ą─├µĘe.

ĪĪĪĪĮŌŻ║Å─Ū░├µĄ─łDą╬╔Ž┐╔ęįų¬Ą└��Ż¼Ū░ę╗éĆĄ╚č³ų▒ĮŪ╚²ĮŪą╬Ą─ā╔éĆŲ┤│╔Ą─š²ĘĮą╬����Ż¼Ą╚ė┌║¾ę╗éĆĄ╚č³ų▒ĮŪ╚²ĮŪą╬╦─éĆŲ┤│╔Ą─š²ĘĮą╬.ę“┤╦║¾ę╗éĆ╚²ĮŪą╬├µĘe╩ŪŪ░ę╗éĆ╚²ĮŪą╬├µĘeĄ─ę╗░ļŻ¼Ą┌ę╗éĆĄ╚č³ų▒ĮŪ╚²ĮŪą╬Ą─├µĘe╩Ū8Ī┴8Ī┬2ŻĮ32.
ĪĪĪĪ▀@ę╗éĆłDą╬Ą─├µĘe╩Ū
ĪĪĪĪ32Ż½16Ż½ 8Ż½ 4 Ż½ 2Ż½1ŻĮ 63.
ĪĪĪĪ└²8 ╚ńėęłD��Ż¼ā╔éĆķLĘĮą╬»BĘ┼į┌ę╗Ų��Ż¼ąĪķLą╬Ą─īÆ╩Ū2���Ż¼A³c╩Ū┤¾ķLĘĮą╬ę╗▀ģĄ─ųą³cŻ¼▓óŪę╚²ĮŪą╬ABC╩ŪĄ╚č³ų▒ĮŪ╚²ĮŪą╬����Ż¼─Ū├┤łDųąĻÄė░▓┐ĘųĄ─┐é├µĘe╩ŪČÓ╔┘Ż┐

ĪĪĪĪĮŌŻ║×ķ┴╦šf├„Ą─ĘĮ▒Ń����Ż¼į┌łD╔Žś╦(bi©Īo)╔Žėó╬─ūų─Ė DŻ¼E��Ż¼F(xi©żn)Ż¼G.
ĪĪĪĪ╚²ĮŪą╬ABCĄ─├µĘe=2Ī┴2Ī┬2ŻĮ2.
ĪĪĪĪ╚²ĮŪą╬ABC����Ż¼ADEŻ¼EFGČ╝╩ŪĄ╚č³ų▒ĮŪ╚²ĮŪą╬.
ĪĪĪĪ╚²ĮŪą╬ABCĄ─ą▒▀ģ�Ż¼┼c╚²ĮŪą╬ADEĄ─ų▒ĮŪ▀ģę╗śėķLŻ¼ę“┤╦╚²ĮŪą╬ ADE├µĘe=ABC├µĘeĪ┴2ŻĮ4.
ĪĪĪĪ╚²ĮŪą╬EFGĄ─ą▒▀ģ┼c╚²ĮŪą╬ABCĄ─ų▒ĮŪ▀ģę╗śėķL.ę“┤╦╚²ĮŪą╬EFG├µĘe=ABC├µĘeĪ┬2ŻĮ1.
ĪĪĪĪĻÄė░▓┐ĘųĄ─┐é├µĘe╩Ū 4Ż½1ŻĮ5.
ĪĪĪĪ└²9 ╚ńėęłD�Ż¼ęčų¬ę╗éĆ╦─▀ģą╬ABCDĄ─ā╔Śl▀ģĄ─ķLČ╚ADŻĮ7Ż¼BCŻĮ3�Ż¼╚²éĆĮŪĄ─Č╚öĄ(sh©┤)Ż║ĮŪ B║═D╩Ūų▒ĮŪŻ¼ĮŪA╩Ū45ĪŃ.Ū¾▀@éĆ╦─▀ģą╬Ą─├µĘe.

ĪĪĪĪĮŌŻ║▀@éĆłDą╬┐╔ęį┐┤ū„╩Ūę╗éĆĄ╚č³ų▒ĮŪ╚²ĮŪą╬ADE�Ż¼ŪąĄ¶ę╗éĆĄ╚č³ų▒ĮŪ╚²ĮŪą╬BCE.
ĪĪĪĪę“×ķ
ĪĪĪĪA╩Ū45ĪŃŻ¼ĮŪD╩Ū90ĪŃ����Ż¼ĮŪE╩Ū
ĪĪĪĪ180ĪŃ-45ĪŃ-90ĪŃŻĮ 45ĪŃŻ¼
ĪĪĪĪ╦∙ęįADE╩ŪĄ╚č³ų▒ĮŪ╚²ĮŪą╬�Ż¼BCEę▓╩ŪĄ╚č³ų▒ĮŪ╚²ĮŪą╬.
ĪĪĪĪ╦─▀ģą╬ABCDĄ─├µĘeŻ¼╩Ū▀@ā╔éĆĄ╚č³ų▒ĮŪ╚²ĮŪą╬├µĘeų«▓Ņ��Ż¼╝┤
ĪĪĪĪ7Ī┴7Ī┬2-3Ī┴3Ī┬2ŻĮ20.
ĪĪĪĪ▀@╩Ū1994ąĪīW(xu©”)öĄ(sh©┤)īW(xu©”)ŖW┴ųŲź┐╦øQ┘ÉįćŅ}.įŁüĒįćŅ}łD╔Ž▓óø]ėą«ŗ│÷╠ōŠĆ╚²ĮŪą╬.ģó┘É═¼īW(xu©”)╩Ū▓╗┤¾╚▌ęūŽļĄĮ░čłDą╬ča╚½│╔×ķĄ╚č³ų▒ĮŪ╚²ĮŪą╬.ę“┤╦ū÷ī”▀@Ą└Ņ}Ą─╚╦öĄ(sh©┤)▓╗ČÓ.Ą½╩Ūėąę╗ą®═¼īW(xu©”)�Ż¼ė├ų▒ŠĆAC░čłDą╬Ęų│╔ā╔éĆų▒ĮŪ╚²ĮŪą╬Ż¼▓óšJ(r©©n)×ķ▀@ā╔éĆų▒ĮŪ╚²ĮŪą╬╩Ūę╗śėĄ─��Ż¼▀@Š═┤¾Õe╠žÕe┴╦.▀@śėū÷���Ż¼ĮŪ A╩Ū 45ĪŃ�Ż¼▀@ę╗Śl╝■▀Ćė├Ą├╔Žå߯┐łDą╬╔ŽŠĆČ╬ŽÓĄ╚��Ż¼ā╔éĆ╚²ĮŪą╬ŽÓĄ╚�����Ż¼╩Ū▓╗─▄┐┐č█Š”üĒ£yČ©Ą─�����Ż¼▒žĒÜÅ─Äū║╬īW(xu©”)╔Žšę│÷Ė∙ō■(j©┤)�Ż¼ąĪīW(xu©”)═¼īW(xu©”)╔ą╬┤īW(xu©”)▀^Äū║╬Ż¼Ū¦╚f▓╗ę¬ļS▒Ńī”łDą╬Ž┬ĮY(ji©”)šō.╬ęéāæ¬(y©®ng)įōÅ─Ņ}─┐ųąęčėąĄ─Śl╝■ū„×ķ╦╝┐╝Ą─ŠĆ╦„.ėą45ĪŃ║═ų▒ĮŪ�Ż¼─Ńæ¬(y©®ng)╩ūŽ╚┐╝æ]Ą╚č³ų▒ĮŪ╚²ĮŪą╬.
ĪĪĪĪ¼F(xi©żn)į┌╬ęéā▐D(zhu©Żn)Ž“š²ĘĮą╬Ą─å¢Ņ}.
ĪĪĪĪ└²10 į┌ėęłD 11Ī┴15Ą─ķLĘĮą╬ā╚(n©©i)Ż¼ėą╦─ī”š²ĘĮą╬Ż©ś╦(bi©Īo)╠¢ŽÓ═¼Ą─ā╔éĆš²ĘĮą╬×ķę╗ī”Ż®���Ż¼├┐ę╗ī”╩ŪŽÓ═¼Ą─š²ĘĮą╬Ż¼─Ū├┤ųąķg▀@éĆąĪš²ĘĮą╬Ż©ĻÄė░▓┐ĘųŻ®├µĘe╩ŪČÓ╔┘�Ż┐

ĪĪĪĪĮŌŻ║ķLĘĮą╬Ą─īÆŻ¼╩ŪĪ░ę╗Ī▒┼cĪ░Č■Ī▒ā╔éĆš²ĘĮą╬Ą─▀ģķLų«║═�Ż¼ķLĘĮą╬Ą─ķLŻ¼╩ŪĪ░ę╗Ī▒�ĪóĪ░╚²Ī▒┼cĪ░Č■Ī▒╚²éĆš²ĘĮą╬Ą─▀ģķLų«║═.
ĪĪĪĪķL-īÆ =15-11ŻĮ4
ĪĪĪĪ╩ŪĪ░╚²Ī▒š²ĘĮą╬Ą─▀ģķL.
ĪĪĪĪīÆėų╩Ūā╔éĆĪ░╚²Ī▒š²ĘĮą╬┼cųąķgąĪš²ĘĮą╬Ą─▀ģķLų«║═�Ż¼ę“┤╦
ĪĪĪĪųąķgąĪš²ĘĮą╬▀ģķL=11-4Ī┴2ŻĮ3.
ĪĪĪĪųąķgąĪš²ĘĮą╬├µĘe=3Ī┴3ŻĮ 9.
ĪĪĪĪ╚ń╣¹░č▀@ę╗łDą╬����Ż¼«ŗį┌ĘĮĖ±╝ł╔ŽŻ¼Š═ę╗─┐┴╦╚╗┴╦.
ĪĪĪĪ└²11 Å─ę╗ēKš²ĘĮą╬═┴Ąžųą�����Ż¼äØ│÷ę╗ēKīÆ×ķ1├ūĄ─ķLĘĮą╬═┴ĄžŻ©ęŖłDŻ®���Ż¼╩ŻŽ┬Ą─ķLĘĮą╬═┴Ąž├µĘe╩Ū15.75ŲĮĘĮ├ū.Ū¾äØ│÷Ą─ķLĘĮą╬═┴ĄžĄ─├µĘe.

ĪĪĪĪĮŌŻ║╩ŻŽ┬Ą─ķLĘĮą╬═┴Ąž�Ż¼╬ęéāęčų¬Ą└
ĪĪĪĪķL-īÆ=1Ż©├ūŻ®.
ĪĪĪĪ▀Ćų¬Ą└╦³Ą─├µĘe╩Ū15.75ŲĮĘĮ├ū�Ż¼─Ū├┤─▄ʱÅ─▀@ę╗├µĘeŪ¾│÷ķL┼cīÆų«║═─žŻ┐
ĪĪĪĪ╚ń╣¹─▄Ū¾│÷��Ż¼─Ū├┤┼c╔Ž├µĪ░▓ŅĪ▒Ą─╦Ń╩ĮŠ═ą╬│╔║═▓Ņå¢Ņ}┴╦.
ĪĪĪĪ╬ęéā░čķL║═īÆŲ┤į┌ę╗Ų�����Ż¼╚ńėęłD.

ĪĪĪĪÅ─▀@éĆłDą╬▀Ć▓╗─▄╦Ń│÷ķL┼cīÆų«║═��Ż¼Ą½╩Ūį┘Ų┤╔Ž═¼śėĄ─ā╔éĆš²ĘĮą╬�Ż¼╚ńŽ┬łDŠ═Ų┤│╔ę╗éĆ┤¾š²ĘĮą╬Ż¼▀@éĆš²ĘĮą╬Ą─▀ģķLŻ¼ŪĪ║├╩ŪķLĘĮą╬Ą─ķL┼cīÆų«║═.

ĪĪĪĪ┐╔╩Ū▀@éĆ┤¾š²ĘĮą╬Ą─ųąķg▀Ćėąę╗éĆ┐šČ┤.╦³ę▓╩Ūę╗éĆš²ĘĮą╬�Ż¼ūą╝Ü(x©¼)ė^▓ņę╗Ž┬Ż¼Š═Ģ■░l(f©Ī)¼F(xi©żn)����Ż¼╦³Ą─▀ģķLŻ¼ŪĪ║├╩ŪķLĘĮą╬Ą─ķL┼cīÆų«▓Ņ����Ż¼Ą╚ė┌1├ū.
ĪĪĪĪ¼F(xi©żn)į┌Ż¼╬ęéāŠ═┐╔ęį╦Ń│÷┤¾š²ĘĮą╬├µĘeŻ║
ĪĪĪĪ15.75Ī┴4+1Ī┴1ŻĮ 64Ż©ŲĮĘĮ├ūŻ®.
ĪĪĪĪ64╩Ū8Ī┴8��Ż¼┤¾š²ĘĮą╬▀ģķL╩Ū 8├ū��Ż¼ę▓Š═╩ŪšfķLĘĮą╬Ą─
ĪĪĪĪķL+īÆ=8Ż©├ūŻ®.
ĪĪĪĪę“┤╦
ĪĪĪĪķL=Ż©8Ż½1Ż®Ī┬2ŻĮ 4.5Ż©├ūŻ®.
ĪĪĪĪīÆ=8-4.5ŻĮ3.5Ż©├ūŻ®.
ĪĪĪĪ─Ū├┤äØ│÷Ą─ķLĘĮą╬├µĘe╩Ū
ĪĪĪĪ4.5Ī┴1ŻĮ4. 5Ż©ŲĮĘĮ├ūŻ®.
ĪĪĪĪ└²12 ╚ńėęłD.š²ĘĮą╬ABCD┼cš²ĘĮą╬EFGC▓óĘ┼į┌ę╗Ų.ęčų¬ąĪš²ĘĮą╬EFGCĄ─▀ģķL╩Ū6�����Ż¼Ū¾╚²ĮŪą╬AEGŻ©ĻÄė░▓┐ĘųŻ®Ą─├µĘe.

ĪĪĪĪĮŌŻ║╦─▀ģą╬AECD╩Ūę╗éĆ╠▌ą╬.╦³Ą─Ž┬Ąū╩ŪAD�Ż¼╔ŽĄū╩ŪECŻ¼Ė▀╩ŪCD����Ż¼ę“┤╦
ĪĪĪĪ╦─▀ģą╬AECD├µĘe=Ż©ąĪš²ĘĮą╬▀ģķL+┤¾š²ĘĮą╬▀ģķLŻ®Ī┴┤¾š²ĘĮą╬▀ģķLĪ┬2
ĪĪĪĪ╚²ĮŪą╬ADG╩Ūų▒ĮŪ╚²ĮŪą╬Ż¼╦³Ą─ę╗Ślų▒ĮŪ▀ģķLDG=Ż©ąĪš²ĘĮą╬▀ģķL+┤¾š²ĘĮą╬▀ģķLŻ®���Ż¼ę“┤╦
ĪĪĪĪ╚²ĮŪą╬ADG├µĘe=Ż©ąĪš²ĘĮą╬▀ģķL+┤¾š²ĘĮą╬▀ģķLŻ®Ī┴┤¾š²ĘĮą╬▀ģķLĪ┬2.
ĪĪĪĪ╦─▀ģą╬ AECD┼c╚²ĮŪą╬ ADG├µĘeę╗śė┤¾.╦─▀ģą╬AHCD╩Ū╦³éāā╔š▀╣▓ėą�Ż¼ę“┤╦��Ż¼╚²ĮŪą╬AEH┼c╚²ĮŪą╬HCG├µĘeŽÓĄ╚�����Ż¼Č╝╝ė╔Ž╚²ĮŪą╬EHG├µĘe║¾��Ż¼Š═ėą
ĪĪĪĪĻÄė░▓┐Ęų├µĘe=╚²ĮŪą╬ECG├µĘe
ĪĪĪĪ=ąĪš²ĘĮą╬├µĘeĄ─ę╗░ļ
ĪĪĪĪ= 6Ī┴6Ī┬2ŻĮ18.
ĪĪĪĪ╩«Ęųėą╚żĄ─╩Ū�����Ż¼ė░ĻÄ▓┐Ęų├µĘe�Ż¼ų╗┼cąĪš²ĘĮą╬▀ģķLėąĻP(gu©Īn)Ż¼Č°┼c┤¾š²ĘĮą╬▀ģķLģsø]ėąĻP(gu©Īn)ŽĄ.
╚²��ĪóŲõ╦¹Ą─├µĘe
ĪĪĪĪ▀@ę╗╣Ø(ji©”)īóų°ųžĮķĮBŪ¾├µĘeĄ─│Żė├╦╝┬Ę║═╝╝Ū╔.ėąą®└²Ņ}┐┤ŲüĒ▓╗ļy��Ż¼Ą½┐╔ęįĮo─Ńåó░l(f©Ī)Ą─ā╚(n©©i)╚▌▓╗╔┘���Ż¼šłūxš▀ūą╝Ü(x©¼)¾wĢ■.
ĪĪĪĪ└²13 «ŗį┌ĘĮĖ±╝ł╔ŽĄ─ę╗éĆė├┤ųŠĆć·│╔Ą─łDą╬Ż©╚ńėęłDŻ®�Ż¼Ū¾╦³Ą─├µĘe.

ĪĪĪĪĮŌŻ║ų▒Įėėŗ╦Ń┤ųŠĆć·│╔Ą─├µĘe╩Ū└¦ļyĄ─�Ż¼╬ęéā═©▀^┐█│²ų▄ć·š²ĘĮą╬║═ų▒ĮŪ╚²ĮŪą╬üĒėŗ╦Ń.
ĪĪĪĪų▄ć·ąĪš²ĘĮą╬ėą3éĆ���Ż¼├µĘe×ķ1Ą─╚²ĮŪą╬ėą5éĆŻ¼├µĘe×ķ1.5Ą─╚²ĮŪą╬ėą1éĆ��Ż¼ę“┤╦ć·│╔├µĘe╩Ū
ĪĪĪĪ4Ī┴4-3-5-1.5ŻĮ6.5.
ĪĪĪĪ└²6┼c▒ŠŅ}į┌ĮŌŅ}╦╝┬Ę╔Ž╩Ū═Ļ╚½ŅÉ═¼Ą─.
ĪĪĪĪ└²14 Ž┬łDųą ABCD╩Ū 6Ī┴8Ą─ķLĘĮą╬���Ż¼AFķL╩Ū4��Ż¼Ū¾ĻÄė░▓┐Ęų╚²ĮŪą╬AEFĄ─├µĘe.

ĪĪĪĪĮŌŻ║╚²ĮŪą╬AEFųą�����Ż¼╬ęéāų¬Ą└ę╗▀ģAF�Ż¼Ą½╩Ū▓╗ų¬Ą└╦³Ą─Ė▀ČÓķL��Ż¼ų▒ĮėŪ¾╦³Ą─├µĘe╩Ū└¦ļyĄ─.╚ń╣¹░č╦³öU┤¾ĄĮ╚²ĮŪą╬AEB���Ż¼Ąū▀ģAB����Ż¼Š═╩ŪķLĘĮą╬Ą─ķL����Ż¼Ė▀╩ŪķLĘĮą╬Ą─īÆ���Ż¼╝┤BCĄ─ķLŻ¼├µĘeŠ═┐╔ęįŪ¾│÷.╚²ĮŪą╬AEBĄ─├µĘe╩ŪķLĘĮą╬├µĘeĄ─ę╗░ļ��Ż¼Č°öU┤¾Ą─╚²ĮŪą╬AFB╩Ūų▒ĮŪ╚²ĮŪą╬����Ż¼╦³Ą─ā╔Ślų▒ĮŪ▀ģĄ─ķL╩Ūų¬Ą└Ą─�����Ż¼║▄╚▌ęū╦Ń│÷╦³Ą─├µĘe.ę“┤╦
ĪĪĪĪ╚²ĮŪą╬AEF├µĘeŻĮŻ©╚²ĮŪą╬ AEB├µĘeŻ®-Ż©╚²ĮŪą╬ AFB├µĘeŻ®
ĪĪĪ����ĪŻĮ8Ī┴6Ī┬2-4Ī┴8Ī┬2
ĪĪĪĪŻĮ 8.
ĪĪĪĪĪĪ▀@ę╗└²Ņ}ĖµįV╬ęéā�Ż¼ėąĢr╬ęéā░čļyŪ¾Ą─łDą╬öU┤¾│╔ęūŪ¾Ą─łDą╬Ż¼«ö(d©Īng)╚╗öU┤¾Ą─▓┐Ęųę▓ę¬╚▌ęūŪ¾│÷��Ż¼Å─Č°ķgĮėĄžĮŌøQ┴╦å¢Ņ}.Ū░├µ└²9Ą─ĮŌĘ©��Ż¼ę▓╩Ū▀@ĘN╦╝┬Ę.
ĪĪĪĪ└²15 Ž┬ū¾łD╩Ūę╗ēKķLĘĮą╬▓▌Ąž����Ż¼ķLĘĮą╬Ą─ķL╩Ū16��Ż¼īÆ╩Ū10.ųąķgėąā╔ŚlĄ└┬Ę���Ż¼ę╗Śl╩ŪķLĘĮą╬Ż¼ę╗Śl╩ŪŲĮąą╦─▀ģą╬��Ż¼─Ū├┤ėą▓▌▓┐ĘųĄ─├µĘeŻ©ĻÄė░▓┐ĘųŻ®ėąČÓ┤¾�����Ż┐
ĪĪ
ĪĪĪĪĮŌŻ║╬ęéā╩ūŽ╚ę¬┼¬ŪÕ│■�����Ż¼ŲĮąą╦─▀ģą╬├µĘeėąČÓ┤¾.ŲĮąą╦─▀ģą╬Ą─├µĘe╩ŪĄūĪ┴Ė▀.Å─łD╔Ž┐╔ęį┐┤│÷�����Ż¼Ąū╩Ū2�Ż¼Ė▀ŪĪ║├╩ŪķLĘĮą╬Ą─īÆČ╚.ę“┤╦▀@éĆŲĮąą╦─▀ģą╬Ą─├µĘe┼c 10Ī┴2Ą─ķLĘĮą╬├µĘeŽÓĄ╚.
ĪĪĪĪ┐╔ęįįO(sh©©)ŽļŻ¼░č▀@éĆŲĮąą╦─▀ģą╬ōQ│╔ 10Ī┴2Ą─ķLĘĮą╬�Ż¼į┘░čÖMžQā╔ŚlČ╝ęŲų┴▀ģ╔ŽŻ©╚ńŪ░ĒōėęłDŻ®Ż¼▓▌Ąž▓┐Ęų├µĘeŻ©ĻÄė░▓┐ĘųŻ®▀Ć╩Ū┼cįŁüĒę╗śė┤¾ąĪ�����Ż¼ę“┤╦
ĪĪĪĪ▓▌Ąž├µĘe=Ż©16-2Ż®Ī┴Ż©10-2Ż®ŻĮ 112.
ĪĪĪĪ└²16 ėęłD╩Ūā╔éĆŽÓ═¼Ą─ų▒ĮŪ╚²ĮŪą╬»Bį┌ę╗ŲŻ¼Ū¾ĻÄė░▓┐ĘųĄ─├µĘe.

ĪĪĪĪĮŌŻ║īŹļH╔Ž���Ż¼ĻÄė░▓┐Ęų╩Ūę╗éĆ╠▌ą╬���Ż¼┐╔╩Ū╦³Ą─╔ŽĄūĪóŽ┬Ąū║═Ė▀Č╝▓╗ų¬Ą└����Ż¼▓╗─▄ų▒ĮėüĒŪ¾╦³Ą─├µĘe.
ĪĪĪĪĻÄė░▓┐Ęų┼c╚²ĮŪą╬BCE║Žį┌ę╗Ų����Ż¼Š═╩ŪįŁų▒ĮŪ╚²ĮŪą╬.─Ń╩Ūʱ┐┤│÷Ż¼ ABCDę▓╩Ū╠▌ą╬����Ż¼╦³║═╚²ĮŪą╬BCE║Žį┌ę╗ŲŻ¼ę▓╩ŪįŁų▒ĮŪ╚²ĮŪą╬.ę“┤╦��Ż¼╠▌ą╬ABCDĄ─├µĘe┼cĻÄė░▓┐Ęų├µĘeę╗śė┤¾.╠▌ą╬ABCDĄ─╔ŽĄūBC�Ż¼╩Ūų▒ĮŪ▀ģADĄ─ķL£p╚ź3Ż¼Ė▀Š═╩ŪDCĄ─ķL.ę“┤╦ĻÄė░▓┐Ęų├µĘeĄ╚ė┌
ĪĪĪĪ╠▌ą╬ ABCD├µĘe=Ż©8Ż½8-3Ż®Ī┴5Ī┬2ŻĮ 32.5.
ĪĪĪĪ╔Ž├µā╔éĆ└²ūėČ╝åó░l(f©Ī)╬ęéā�Ż¼╚ń║╬░č▓╗╚▌ęū╦ŃĄ─├µĘeŻ¼ōQ│╔╚▌ęū╦ŃĄ─├µĘe��Ż¼öĄ(sh©┤)īW(xu©”)╔Ž▀@ĮąĄ╚Ęeūāą╬.ꬎļėą▀@ĘNĪ░ōQĪ▒Ą─▒ŠŅI(l©½ng)Ż¼╩ūŽ╚ę¬╠ßĖ▀ī”łDą╬Ą─ė^▓ņ─▄┴”.
ĪĪĪĪ└²17 Ž┬łD╩Ūā╔éĆų▒ĮŪ╚²ĮŪą╬»BĘ┼į┌ę╗Ųą╬│╔Ą─łDą╬.ęčų¬ AF���Ż¼F(xi©żn)E�Ż¼ECČ╝Ą╚ė┌3���Ż¼ CB�����Ż¼ BDČ╝Ą╚ė┌ 4.Ū¾▀@éĆłDą╬Ą─├µĘe.
ĪĪĪĪĮŌŻ║ā╔éĆų▒ĮŪ╚²ĮŪą╬Ą─├µĘe╩Ū║▄╚▌ęūŪ¾│÷Ą─.

ĪĪĪĪ╚²ĮŪą╬ABC├µĘe=Ż©3Ż½3Ż½3Ż®Ī┴4Ī┬2ŻĮ18.
ĪĪĪĪ╚²ĮŪą╬CDE├µĘe=Ż©4Ż½4Ż®Ī┴ 3Ī┬2ŻĮ12.
ĪĪĪĪ▀@ā╔éĆų▒ĮŪ╚²ĮŪą╬ėąę╗éĆųž»B▓┐Ęų--╦─▀ģą╬BCEG����Ż¼ų╗ę¬£p╚ź▀@éĆųž»B▓┐Ęų����Ż¼╦∙Ū¾łDą╬Ą─├µĘe┴ó╝┤┐╔ęįĄ├│÷.
ĪĪĪĪę“×ķ AFŻĮ FEŻĮ ECŻĮ3Ż¼╦∙ęį AGF�����Ż¼ FGE��Ż¼ EGC╩Ū╚²éĆ├µĘeŽÓĄ╚Ą─╚²ĮŪą╬.
ĪĪĪĪę“×ķCBŻĮBDŻĮ4Ż¼╦∙ęįCGB��Ż¼BGD╩Ūā╔éĆ├µĘeŽÓĄ╚Ą─╚²ĮŪą╬.
ĪĪĪĪ2Ī┴╚²ĮŪą╬DEC├µĘe
ĪĪĪĪ= 2Ī┴2Ī┴Ż©╚²ĮŪą╬ GBC├µĘeŻ®Ż½2Ī┴Ż©╚²ĮŪą╬ GCE├µĘeŻ®.
ĪĪĪĪ╚²ĮŪą╬ABC├µĘe
ĪĪĪĪ= Ż©╚²ĮŪą╬ GBC├µĘeŻ®Ż½3Ī┴Ż©╚²ĮŪą╬GCE├µĘeŻ®.
ĪĪĪĪ╦─▀ģą╬BCEG├µĘe
ĪĪĪĪ=Ż©╚²ĮŪą╬GBC├µĘeŻ®Ż½Ż©╚²ĮŪą╬GCE├µĘeŻ®
ĪĪĪĪ=Ż©2Ī┴12Ż½18Ż®Ī┬5
ĪĪĪ�ĪŻĮ8.4.
ĪĪĪĪ╦∙Ū¾łDą╬├µĘe=12Ż½ 18- 8.4ŻĮ21.6.
ĪĪĪĪ└²18 ╚ńŽ┬Ēōū¾łDŻ¼ABCG╩Ū4Ī┴7ķLĘĮą╬�Ż¼DEFG╩Ū 2Ī┴10ķLĘĮą╬.Ū¾╚²ĮŪą╬ BCM┼c╚²ĮŪą╬ DEM├µĘeų«▓Ņ.
ĪĪĪĪĮŌŻ║╚²ĮŪą╬BCM┼cĘŪĻÄė░▓┐Ęų║ŽŲüĒ╩Ū╠▌ą╬ABEF.╚²ĮŪą╬DEM┼cĘŪĻÄė░▓┐Ęų║ŽŲüĒ╩Ūā╔éĆķLĘĮą╬Ą─║═.
ĪĪĪĪŻ©╚²ĮŪą╬BCM├µĘeŻ®-Ż©╚²ĮŪą╬DEM├µĘeŻ®
ĪĪĪĪ=Ż©╠▌ą╬ABEF├µĘeŻ®-Ż©ā╔éĆķLĘĮą╬├µĘeų«║═
ĪĪĪĪ=Ż©7Ż½10Ż®Ī┴Ż©4Ż½2Ż®Ī┬2-Ż©4Ī┴7 Ż½ 2Ī┴10Ż®
ĪĪĪĪ=3.


ĪĪĪĪ└²19 ╔ŽėęłDųą�����Ż¼į┌ķLĘĮą╬ā╚(n©©i)«ŗ┴╦ę╗ą®ų▒ŠĆ��Ż¼ęčų¬▀ģ╔Žėą╚²ēK├µĘeĘųäe╩Ū13�����Ż¼35��Ż¼49.─Ū├┤łDųąĻÄė░▓┐ĘųĄ─├µĘe╩ŪČÓ╔┘��Ż┐
ĮŌŻ║╦∙Ū¾Ą─ė░ĻÄ▓┐Ęų�Ż¼ŪĪ║├╩Ū╚²ĮŪą╬ABC┼c╚²ĮŪą╬CDEĄ─╣½╣▓▓┐Ęų�����Ż¼Č°├µĘe×ķ13���Ż¼49�����Ż¼35▀@╚²ēK╩ŪķLĘĮą╬ųąø]ėą▒╗╚²ĮŪą╬ABC┼c╚²ĮŪą╬CDE╔wūĪĄ─▓┐Ęų�Ż¼ę“┤╦
ĪĪĪĪŻ©╚²ĮŪą╬ ABC├µĘeŻ®+Ż©╚²ĮŪą╬CDE├µĘeŻ®Ż½Ż©13Ż½49Ż½35Ż®
ĪĪĪ�����ĪŻĮŻ©ķLĘĮą╬├µĘeŻ®Ż½Ż©ĻÄė░▓┐Ęų├µĘeŻ®.
ĪĪĪĪ╚²ĮŪą╬ABC����Ż¼Ąū╩ŪķLĘĮą╬Ą─ķLŻ¼Ė▀╩ŪķLĘĮą╬Ą─īÆ�����Ż╗╚²ĮŪą╬CDE��Ż¼Ąū╩ŪķLĘĮą╬Ą─īÆ����Ż¼Ė▀╩ŪķLĘĮą╬Ą─ķL.ę“┤╦Ż¼╚²ĮŪą╬ABC├µĘeŻ¼┼c╚²ĮŪą╬CDE├µĘe����Ż¼Č╝╩ŪķLĘĮą╬├µĘeĄ─ę╗░ļŻ¼Š═ėą
ĪĪĪĪĻÄė░▓┐Ęų├µĘe=13 Ż½ 49Ż½ 35ŻĮ 97.





